N-Queens
June 11, 2010
We present today a classic exercise that has been on my to-do list since the start of Programming Praxis.
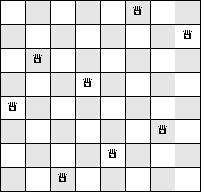
The n-queens problem is to find all possible ways to place n queens on an n × n chess board in such a way that no two queens share a row, column, or diagonal. The diagram at right shows one way that can be done on a standard 8 × 8 chess board.
Your task is to write a program to find all such placements. When you are finished, you are welcome to read or run a suggested solution, or to post your own solution or discuss the exercise in the comments below.
Programming Praxis 
My Haskell solution (see http://bonsaicode.wordpress.com/2010/06/11/programming-praxis-n-queens/ for a version with comments):
import Data.List queens :: Int -> [[Int]] queens n = filter (safe . zip [1..]) $ permutations [1..n] safe :: [(Int, Int)] -> Bool safe [] = True safe (x:xs) = all (safe' x) xs && safe xs where safe' (x1,y1) (x2,y2) = x1+y1 /= x2+y2 && x1-y1 /= x2-y2[…] Praxis – N-Queens By Remco Niemeijer In today’s Programming Praxis we have to solve the classic n-queens problem. The provided Scheme solution has […]
I was trying to make a version that printed and counted, and would fit in 4 lines so you could use it as a .signature file. Didn’t quite succeed, mostly because I need to include to get printf, but here’s where I got it.
#include <stdio.h> int t,i,j,b[8],r;c(){r=1;for(i=0;i<7;i++)for(j=i+1;j<8;j++)r&=(b[i]-b[j]&&abs(i -j)!=abs(b[i]-b[j]));return r;}p(){for(i=0;i<8;i++){for(j=0;j<8;j++)putchar( " Q"[j==b[i]]);puts("");}puts("");t++;}s(n){int i;if(n--){for(i=8;i;){b[n]=--i; s(n);}}else if(c(b))p(b);}main(){s(8);printf("%d solutions.\n",t);}N = 8
def valid? stack
q2 = stack.length – 1
(0..stack.length-2).each do |q1|
return false if stack[q1] == stack[q2] ||
(q1-q2).abs == (stack[q1]-stack[q2]).abs
end
end
def queens stack, n
if n == N
puts “[ #{stack.join(‘, ‘)} ]”
else
(1..N).each do |rank|
stack.push(rank)
queens(stack, n+1) if valid?(stack)
stack.pop
end
end
end
queens [], 0
Here’s a ruby version (commented at http://steamcode.blogspot.com/2010/06/n-queens-problem-in-ruby.html)
class Board def initialize(n) @n = n @board = Array.new(n) @board.map! { Array.new(n, "b") } end def print_board puts "Board:" @board.each_index do |row| @board.each_index do |col| end puts end end def safe_row(suggested_row) 0.upto(@n-1) do |col| return false if @board[suggested_row][col] == "Q" end return true end def safe_col(suggested_col) 0.upto(@n-1) do |row| return false if @board[row][suggested_col] == "Q" end return true end def safe_diag(suggested_row, suggested_col, row_mod, col_mod) row,col = suggested_row+row_mod, suggested_col+col_mod while true do break if (row >= @n) || (col >= @n) || (row < 0) || (col < 0) return false if @board[row][col] == "Q" row += row_mod col += col_mod end return true end def safe(suggested_row, suggested_col) return false if !safe_row(suggested_row) return false if !safe_col(suggested_col) return false if !safe_diag(suggested_row, suggested_col, 1, 1) return false if !safe_diag(suggested_row, suggested_col, 1, -1) return false if !safe_diag(suggested_row, suggested_col, -1, 1) return false if !safe_diag(suggested_row, suggested_col, -1, -1) return true end def solve solve_1(0) end def solve_1(row) 0.upto(@n-1) do |col| if safe(row, col) @board[row][col] = "Q" if row == (@n-1) print_board else solve_1(row+1) end @board[row][col] = "b" end end end end board = Board.new(8).solvehttp://en.wikipedia.org/wiki/Eight_queens_puzzle section ‘constructing a solution’ shows an algorithm that is linear in the number of columns of the board when implemented with a vector. It allows you to go to boardsizes up to N=200000000 (I can’t go higher because of memory)
(define (queens N) (if (and (exact-nonnegative-integer? N) (> N 3)) (let* ((R (remainder N 12)) (n-even (floor (/ N 2))) (n-odd (- N n-even)) (V (make-vector N)) (set-V! (lambda (f r) (vector-set! V f r))) (sema (make-semaphore 0))) (let-syntax ((do-loop (syntax-rules () ((for (x range ...) body ...) (for ((x (in-range range ...))) body ...))))) (thread (λ () (case R ((3 9) (do-loop (F 0 (sub1 n-even)) (set-V! F (+ (* 2 F) 3))) (set-V! (sub1 n-even) 1)) (else (do-loop (F 0 n-even) (set-V! F (add1 (* 2 F)))))) (semaphore-post sema))) ; Signal completion. (thread (λ () (case R ((2) (do-loop (F 2 (- n-odd 1)) (set-V! (+ F n-even) (+ (* 2 F) 2))) (set-V! n-even 2) (set-V! (add1 n-even) 0) (set-V! (sub1 N) 4)) ((3 9) (do-loop (F 0 (- n-odd 2)) (set-V! (+ F n-even) (+ (* 2 F) 4))) (set-V! (- N 2) 0) (set-V! (sub1 N) 2)) ((8) (do-loop (i 0 (sub1 n-odd) 2) (set-V! (+ i n-even) (* 2 (add1 i))) (set-V! (+ i n-even 1) (* 2 i)))) (else (do-loop (F 0 n-odd) (set-V! (+ F n-even) (* 2 F))))) (semaphore-post sema))) ; Signal completion. (semaphore-wait sema) ; Wait for both loops to complete. (semaphore-wait sema) V)) (raise-type-error 'queens "exact integer greater than 3" N)))Another usefull website about the N queens problem is http://sites.google.com/site/nqueensolver/
which has algorithms and executables for download
Here’s a different, somewhat simpler, solution in Scheme:
(define (attack? q1 q2)(or (= (car q1) (car q2))
(= (cadr q1) (cadr q2))
(= (abs (- (car q1) (car q2)))
(abs (- (cadr q1) (cadr q2))))))
(define (safe? q qs)(cond ((null? qs) #t)
((attack? q (car qs)) #f)
(else (safe? q (cdr qs)))))
(define (queens n)(let queen ((n n) (x 1) (y 1) (qs '()) (qss '()))
(cond ((< n x) (cons (reverse qs) qss))
((< n y) qss)
((safe? (list x y) qs)
(queen n x (+ y 1) qs
(queen n (+ x 1) 1
(cons (list x y) qs) qss)))
(else (queen n x (+ y 1) qs qss)))))
Java implementation:
Source
can any one tell me how to convert n-queens problem to exact cover problem?
Knuth discusses this in his dancing links paper.
[…] problem with n queens on an n by n chessboard. After finding it again in older posts on both Programming Praxis and DataGenetics, I decided to go ahead and take a crack at it and I think the solution is pretty […]
Hi I am new to Ruby,I wrote a program in ruby which based on NQueen java program by Robert Sedgewick and Kevin Wayne http://introcs.cs.princeton.edu/java/23recursion/Queens.java.html,The problem is My program is not outputting the result,please help me here
my program source : http://repl.it/1jv