Sparse Sets

March 9, 2012

We look today at a clever data structure for storing sparse sets of integers on the range 0 .. u−1 and performing initialization, lookup, and insertion is time O(1) and iteration in O(n), where n is the number of elements in the set. The data structure was studied in a 1993 article “An Efficient Representation for Sparse Sets” by Preston Briggs and Linda Torczon, in Exercise 1.9 (1.8 in the first edition) of Jon Bentley’s book Programming Pearls, and in exercise 2.12 of the 1974 book The Design and Analysis of Computer Algorithms by Al Aho, John Hopcroft and Jeffrey Ullman; the data structure itself dates to the folklore of computing.

The data structure considers a universe of integers from 0 to u−1; depending on the circumstances, the integers probably map to something else, but we don’t care about that. Any given set consists of n items chose from the universe; there are no duplicates. Note that n ≤ u, certainly, and likely n is much less than u — otherwise, you would probably use a bit vector to represent the set. Note also that we are optimizing for speed at the expense of space, as a bit vector takes u bits but our data structure takes 2u integers.

Think about a bit vector. Setting a bit is a constant-time operation, as is checking if a bit is set or unset. But initializing the bit vector and iterating over the set elements of the bit vector each take time proportional to the size of the bit vector. Our sparse sets reduce the iteration to time proportional to the size of the set (rather than the size of the universe) and reduce the initialization time to a constant.

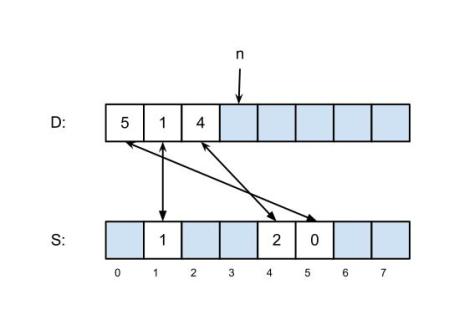
The sparse set is represented by two vectors that we will call dense (abbreviated D) and sparse (abbreviated S). Initially n, the number of elements in the set, is zero; the two vectors are uninitialized and may contain anything. To add an element 0 ≤ k < u to a set that does not already contain k, we set D[n] to k, S[k] to n, and increase n by 1, an operation that takes constant time. After this, the two vectors point to each other, which gives a test of set membership that also works in constant time: an element k is in the set if and only if S[k] < n and D[S[k]] == k>. Note that if k is not a member of the set, the value of S[k] doesn’t matter; either it S[k] will be greater than n or it will point to an element of D that doesn’t point back to it. The diagram above right shows a set with the elements 5, 1 and 4; the blue boxes may contain any value. To iterate over the elements of the set, read D[0 .. n−1], which takes time O(n), and to clear the set make n = 0, which takes time O(1); note in particular that clearing the set doesn’t require reinitialization. Other operations, including size-of, delete, union, intersection, difference, and set-equality are possible, and equally time-efficient compared to bit vectors, but we won’t discuss them here, since they are seldom used with this representation of sets. A common use of these sparse sets is with register allocation algorithms in compilers, which have a fixed universe (the number of registers in the machine) and are updated and cleared frequently during a single processing run.

Your task is to implement the insert, lookup, iterate and clear operations for sparse sets as described above. When you are finished, you are welcome to read or run a suggested solution, or to post your own solution or discuss the exercise in the comments below.

Posted by programmingpraxis

Filed in Exercises

8 Comments »

8 Responses to “Sparse Sets”

Jussi Piitulainen said

March 9, 2012 at 2:10 PM

Thanks, this was a good thing to learn.

Instead of D, S, n, u global, I packaged them in a single vector. This may not be appropriate when a program needs to manipulate a single such set very fast, but with a sufficiently smart compiler …

(define (make-sparse-set u) (make-vector (+ u u 1) 0))            ;DSn, n=0
(define (sparse-size set) (vector-ref set (- (vector-length set) 1))) ;n
(define (sparse-cap set) (quotient (vector-length set) 2))            ;u
(define (dense-ref set k) (vector-ref set k))                         ;D[k]
(define (sparse-ref set k) (vector-ref set (+ (sparse-cap set) k)))   ;S[k]
(define (sparse-member? k set)
  (and (< (sparse-ref set k) (sparse-size set))                   ;S[k] < n
       (= (dense-ref set (sparse-ref set k)) k)))              ;D[S[k]] = k
(define (sparse-insert! set k)
  (if (sparse-member? k set) (error '!))
  (vector-set! set (sparse-size set) k)                          ;D[n] <- k
  (vector-set! set (+ (sparse-cap set) k) (sparse-size set))     ;S[k] <- n
  (vector-set! set (- (vector-length set) 1) (+ (sparse-size set) 1))) ;++n
(define (sparse-for-each proc set)
  (do ((k 0 (+ k 1))) ((= k (sparse-size set))) (proc (vector-ref set k))))
(define (sparse-clear! set) (vector-set! set (- (vector-length set) 1) 0))

Paul G. said
March 9, 2012 at 2:16 PM
here is a Perl version:

use warnings;
use strict;

my @dense;
my @sparse;
my $n;

sub get_number {
my $op = shift;
my $k;
do {
print "Enter number to $op: ";
$k = <STDIN>;
chomp($k);
} while ($k !~ /^\d+$/);
return $k;
}

sub sparse_clear {
$n = 0;
}

sub sparse_insert {
my $k = get_number(‘insert’);
$dense[$n] = $k;
$sparse[$k] = $n;
$n++;
}

sub sparse_lookup {
my $k = get_number(‘lookup’);
( defined($sparse[$k]) &&
($sparse[$k] < $n) &&
($dense[$sparse[$k]] == $k)
) ? print "exists\n" : print "doesn’t exist\n";
}

sub sparse_iterate {
my $largest_sparce = 0;
print "Dense: ";
for (0 .. $n-1) {
print "$dense[$_] ";
$largest_sparce = $dense[$_] if ($dense[$_] > $largest_sparce);
}
print "\n";
print "Sparse ";
for (0 .. $largest_sparce) {
defined($sparse[$_]) ? print "$sparse[$_] " : print "u ";
}
print "\n";
}

sub sparse_quit {
exit;
}

my @ops = qw(clear insert lookup iterate quit);
while(1) {
print "\n";
for (0 .. scalar(@ops)-1) {
print "$_: $ops[$_]\n";
}
print "Enter operation: ";

my $choice = <STDIN>;
chomp($choice);
if ($choice =~ /^[0-4]$/) {
&{\&{"sparse_$ops[$choice]"}}();
}
}

Of course, the easier (and arguably better) way to do this would be to use one of the many existing perl modules which already implement sparse matrix arithmetic: http://search.cpan.org/search?query=sparse&mode=all
ardnew said
March 9, 2012 at 3:38 PM
Very cool post. We often deal with large sparse data structures at work, but unfortunately our bottleneck is typically available memory and not processing time. Something like this is ideal for modern hardware though.

Just to emphasize your note, the maintenance of the variable n is crucial. Not only does it allow for constant-time initialization, clearing, and element-counting, but it is also the only way to guarantee all elements in the universe have unambiguous values.

Definitely going to give this a try sometime this weekend, thanks for sharing!
Joe Taylor said
March 9, 2012 at 4:59 PM
And C#:

using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace SparseSet
{
internal sealed class SparseSet : IEnumerable
{
private ushort?[] D = new ushort?[ushort.MaxValue];
private ushort?[] S = new ushort?[ushort.MaxValue];
private ushort _size = 0;
internal bool Insert(ushort value)
{
bool result = !Lookup(value);
if (result)
{
D[_size] = value;
S[value] = _size;
_size++;
}
return result;
}

internal bool Lookup(ushort value)
{
bool result = S[value] < _size &&
S[value].HasValue &&
D[S[value].Value] == value;
return result;
}

internal void Clear()
{
_size = 0;
}

public IEnumerator GetEnumerator()
{
var result = new SparseSetEnumerator(D, _size);
return result;
}

System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return (IEnumerator)GetEnumerator();
}
}
internal sealed class SparseSetEnumerator : IEnumerator
{
private readonly ushort?[] _values = null;
private readonly ushort _size = 0;
private int _index = -1;
internal SparseSetEnumerator(ushort?[] values, ushort size)
{
_values = values;
_size = size;
}
public ushort Current
{
get
{
return _values[_index].Value;
}
}

public void Dispose()
{
// squeclh
}

object IEnumerator.Current
{
get
{
return (object)_values[_index];
}
}

public bool MoveNext()
{
_index++;
bool moving = _index < _size &&
_values[_index].HasValue;
return moving;
}

public void Reset()
{
_index = -1;
}
}
class Program
{
static void Main(string[] args)
{
var ss = new SparseSet();
ss.Insert(5);
ss.Insert(1);
ss.Insert(4);
ss.Clear();

ss.Insert(5);
ss.Insert(1);
ss.Insert(4);
ss.Clear();

ss.Insert(3);
ss.Insert(2);
ss.Insert(7);
ss.Clear();

ss.Insert(3);
ss.Insert(2);
ss.Insert(7);
ss.Insert(3);
ss.Insert(2);
ss.Insert(7);
ss.Clear();

ss.Insert(3);
ss.Insert(2);
ss.Insert(7);
ss.Insert(5);
ss.Insert(1);
ss.Insert(4);

foreach(ushort us in ss)
{
Console.WriteLine(us);
}
Console.WriteLine("—");
foreach (ushort us in ss)
{
Console.WriteLine(us);
}

ss.Clear();
Console.WriteLine("—");
foreach (ushort us in ss)
{
Console.WriteLine(us);
}
}
}
}

dulanovdulanov said

March 9, 2012 at 9:16 PM

#!/usr/bin/env escript

-export([main/1]).

make_set(U) ->
    {0, array:new(U, {fixed, true}), array:new(U, {fixed, true})}.

clear({_N, D, S}) ->
    {0, D, S}.

insert({N, D, S}, El) ->
    NewD = array:set(N, El, D),
    NewS = array:set(El, N, S),
    {N + 1, NewD, NewS}.

is_member({N, D, S}, El) ->
    Indx = array:get(El, S),
    (Indx < N) andalso (array:get(Indx, D) =:= El).

get_d({_N, D, _S}) ->
    array:to_list(D).

get_s({_N, _D, S}) ->
    array:to_list(S).

for_all({N, D, _S}, Fn) when is_function(Fn) ->
    lists:map(Fn, lists:sublist(array:to_list(D), N)).

main([]) ->
    Set1 = make_set(8),
    Set2 = clear(Set1),
    Set3 = insert(Set2, 5),
    Set4 = insert(Set3, 1),
    Set5 = insert(Set4, 4),
    io:format("~p~n", [is_member(Set5, 0)]),
    io:format("~p~n", [is_member(Set5, 1)]),
    io:format("~p~n", [is_member(Set5, 2)]),
    io:format("~p~n", [is_member(Set5, 3)]),
    io:format("~p~n", [is_member(Set5, 4)]),
    io:format("~p~n", [is_member(Set5, 5)]),
    io:format("~p~n", [is_member(Set5, 6)]),
    io:format("~p~n", [is_member(Set5, 7)]),
    io:format("~p~n", [get_d(Set5)]),
    io:format("~p~n", [get_s(Set5)]),
    for_all(Set5, fun(El) -> io:format(">>> ~p~n", [El]) end).

false
true
false
false
true
true
false
false
[5,1,4,undefined,undefined,undefined,undefined,undefined]
[undefined,1,undefined,undefined,2,0,undefined,undefined]
>>> 5
>>> 1
>>> 4

keenbug said

March 10, 2012 at 11:11 AM

An implementation in Guile (Scheme):

(also here: https://gist.github.com/2011167)

(define-module (programming-praxis sparse-sets)
  #:use-module (srfi srfi-9)
  #:export (make-sparse-set sparse-set-member? sparse-set-add! sparse-set-remove! sparse-set-for-each)
  )

(define-record-type sparse-set
  (%make-sparse-set len dense sparse)
  sparse-set?
  (len sparse-set-len sparse-set-len-set!)
  (dense sparse-set-dense)
  (sparse sparse-set-sparse))


(define (make-sparse-set universe)
  (%make-sparse-set
    0
    (make-vector universe 0)
    (make-vector universe 0)))

(define (sparse-set-sparse-ref set n)
  (vector-ref (sparse-set-sparse set) n))

(define (sparse-set-sparse-set! set n x)
  (vector-set! (sparse-set-sparse set)
               n
               x))

(define (sparse-set-dense-ref set n)
  (vector-ref (sparse-set-dense set) n))

(define (sparse-set-dense-set! set n x)
  (vector-set! (sparse-set-dense set)
               n
               x))

(define (sparse-set-universe set)
  (vector-length (sparse-set-sparse set)))




(define (sparse-set-member? set elem)
  (if (>= elem (sparse-set-universe set))
    (scm-error 'wrong-type-arg
               'sparse-set-add!
               "~S not in universe"
               (list elem)
               #f))
  (let* ((dense-pos (sparse-set-sparse-ref set elem))
         (sparse-pos (sparse-set-dense-ref set dense-pos)))
    (and (< dense-pos (sparse-set-len set))
         (= sparse-pos elem))))

(define (sparse-set-add! set elem)
  (if (>= elem (sparse-set-universe set))
    (scm-error 'wrong-type-arg
               'sparse-set-add!
               "~S not in universe"
               (list elem)
               #f))
  (if (not (sparse-set-member? set elem))
      (let ((pos (sparse-set-len set)))
        (sparse-set-len-set! set (1+ pos))
        (sparse-set-dense-set! set pos elem)
        (sparse-set-sparse-set! set elem pos)))
  set)

(define (sparse-set-remove! set elem)
  (if (>= elem (sparse-set-universe set))
    (scm-error 'wrong-type-arg
               'sparse-set-add!
               "~S not in universe"
               (list elem)
               #f))
  (if (sparse-set-member? set elem)
      (let ((dense-pos (sparse-set-sparse-ref set elem))
            (last-elem (sparse-set-dense-ref set (1- (sparse-set-len set)))))
        (sparse-set-dense-set! set dense-pos last-elem)
        (sparse-set-sparse-set! set last-elem dense-pos)
        (sparse-set-len-set! set (1- (sparse-set-len set)))))
  set)

(define (sparse-set-for-each proc set)
  (let ((len (sparse-set-len set)))
    (do ((i 0 (1+ i)))
        ((= i len))
      (proc (sparse-set-dense-ref set i)))))

Marcel Hendrix said
March 25, 2012 at 11:04 AM
Here is how to do this in Forth. Execute the name of the set to bring it in context.
The INSERT, LOOKUP, ITERATE and SCLEAR words work on the set in context.

0 VALUE #universe
0 VALUE n
0 VALUE Dense
0 VALUE Sparse

: SPARSE-SET ( sz | “name” — )
CREATE DUP , 2* CELLS ALLOT
DOES> @+ TO #universe TO Dense
Dense #universe CELLS + TO Sparse ;

#16 SPARSE-SET test-set

test-set ( make current )

: INSERT ( x — )
DUP #universe >= ABORT” INSERT :: out of range”
DUP Dense n CELL[] !
Sparse []CELL n SWAP !
1 +TO n ;

: LOOKUP ( x — bool )
>R
Sparse R@ CELL[] @ DUP n U>= IF DROP -R FALSE EXIT ENDIF
Dense []CELL @ R> = ;

: ITERATE ( xt — )
LOCAL xt
n 0 ?DO Dense I CELL[] @ xt EXECUTE LOOP ;

: SCLEAR ( — ) CLEAR n ;

SCLEAR
CR .( Insert {5,4,1} ) 5 INSERT 1 INSERT 4 INSERT
CR .( Lookup {5,1,4,15,12} => ) 5 LOOKUP . 1 LOOKUP . 4 LOOKUP . #15 LOOKUP . #12 LOOKUP .
CR .( Iterate with ‘.’ => ) ‘ . ITERATE

:ABOUT CR .” Sparse Sets”
CR .” Try: ( n — ) INSERT”
CR .” ( n — bool ) LOOKUP ”
CR .” ( xt — ) ITERATE ”
CR .” ( — ) SCLEAR ” ;

.ABOUT -sparseset CR
DEPRIVE
Get our problem straigt | ecs.rs 1 – Boris Kostadinov – Multimedia said
February 23, 2023 at 10:48 AM
[…] we created is called a sparse set, and allows for fairly quick acces times and single component […]

S	M	T	W	T	F	S
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

Programming Praxis

Sparse Sets

March 9, 2012

8 Responses to “Sparse Sets”

Leave a comment

Categories

Archives

Archives

Programming Praxis

Sparse Sets

March 9, 2012

Share this:

Related

8 Responses to “Sparse Sets”

Leave a comment

Categories

Archives

Archives